Provides the symmetrized and thresholded matrix of cohesion values.
Arguments
- c
A
cohesion_matrixobject, a matrix of cohesion values (seecohesion_matrix).- symmetric
Logical. Whether the returned matrix should be made symmetric (using the minimum); the default is
TRUE.
Value
The symmetrized cohesion matrix in which all entries corresponding to weak ties are set to zero.
Details
The threshold is that provided by strong_threshold (and is equal to half of
the average of the diagonal of c).
Values of the cohesion matrix which are less than the threshold are set to
zero.
The symmetrization, if desired, is computed using the entry-wise (parallel)
minimum of C and its transpose (i.e., min(C_ij, C_ji)).
The matrix provided by cohesion_strong (with default symmetric = TRUE) is
the adjacency matrix for the graph of strong ties (the cluster graph), see
community_graphs and pald.
Examples
C <- cohesion_matrix(dist(exdata2))
strong_threshold(C)
#> [1] 0.06194614
cohesion_strong(C)
#> 1 2 3 4 5 6 7
#> 1 0.14836219 0.07563492 0.06280664 0.09280664 0.11169553 0.00000000 0.0000000
#> 2 0.07563492 0.13119048 0.06230159 0.07563492 0.08947330 0.00000000 0.0000000
#> 3 0.06280664 0.06230159 0.12082011 0.07748677 0.06280664 0.00000000 0.0000000
#> 4 0.09280664 0.07563492 0.07748677 0.13304233 0.06280664 0.00000000 0.0000000
#> 5 0.11169553 0.08947330 0.06280664 0.06280664 0.14502886 0.00000000 0.0000000
#> 6 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.11577201 0.0000000
#> 7 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.1025661
#> 8 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.0000000
#> 9 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.08225783 0.0000000
#> 10 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.0000000
#> 11 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.0000000
#> 12 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.0000000
#> 13 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.0000000
#> 14 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.0000000
#> 15 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.0000000
#> 16 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.0000000
#> 8 9 10 11 12 13 14
#> 1 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> 2 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> 3 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> 4 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> 5 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> 6 0.0000000 0.08225783 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> 7 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> 8 0.1054762 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> 9 0.0000000 0.11559117 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> 10 0.0000000 0.00000000 0.11990741 0.07702381 0.00000000 0.06765873 0.00000000
#> 11 0.0000000 0.00000000 0.07702381 0.13257937 0.00000000 0.09924603 0.00000000
#> 12 0.0000000 0.00000000 0.00000000 0.00000000 0.11302503 0.07746947 0.06746947
#> 13 0.0000000 0.00000000 0.06765873 0.09924603 0.07746947 0.13988095 0.00000000
#> 14 0.0000000 0.00000000 0.00000000 0.00000000 0.06746947 0.00000000 0.13194444
#> 15 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.09230159
#> 16 0.0000000 0.00000000 0.06435185 0.00000000 0.00000000 0.00000000 0.00000000
#> 15 16
#> 1 0.00000000 0.00000000
#> 2 0.00000000 0.00000000
#> 3 0.00000000 0.00000000
#> 4 0.00000000 0.00000000
#> 5 0.00000000 0.00000000
#> 6 0.00000000 0.00000000
#> 7 0.00000000 0.00000000
#> 8 0.00000000 0.00000000
#> 9 0.00000000 0.00000000
#> 10 0.00000000 0.06435185
#> 11 0.00000000 0.00000000
#> 12 0.00000000 0.00000000
#> 13 0.00000000 0.00000000
#> 14 0.09230159 0.00000000
#> 15 0.12563492 0.00000000
#> 16 0.00000000 0.10145503
#> attr(,"class")
#> [1] "cohesion_matrix" "matrix" "array"
## To illustrate the calculation performed
C_strong <- C
## C_strong is equal to cohesion_strong(C, symmetric = FALSE)
C_strong[C < strong_threshold(C)] <- 0
## C_strong_sym is equal to cohesion_strong(C)
C_strong_sym <- pmin(C_strong, t(C_strong))
## The (cluster) graph whose adjacency matrix, CS,
## is the matrix of strong ties
CS <- cohesion_strong(C)
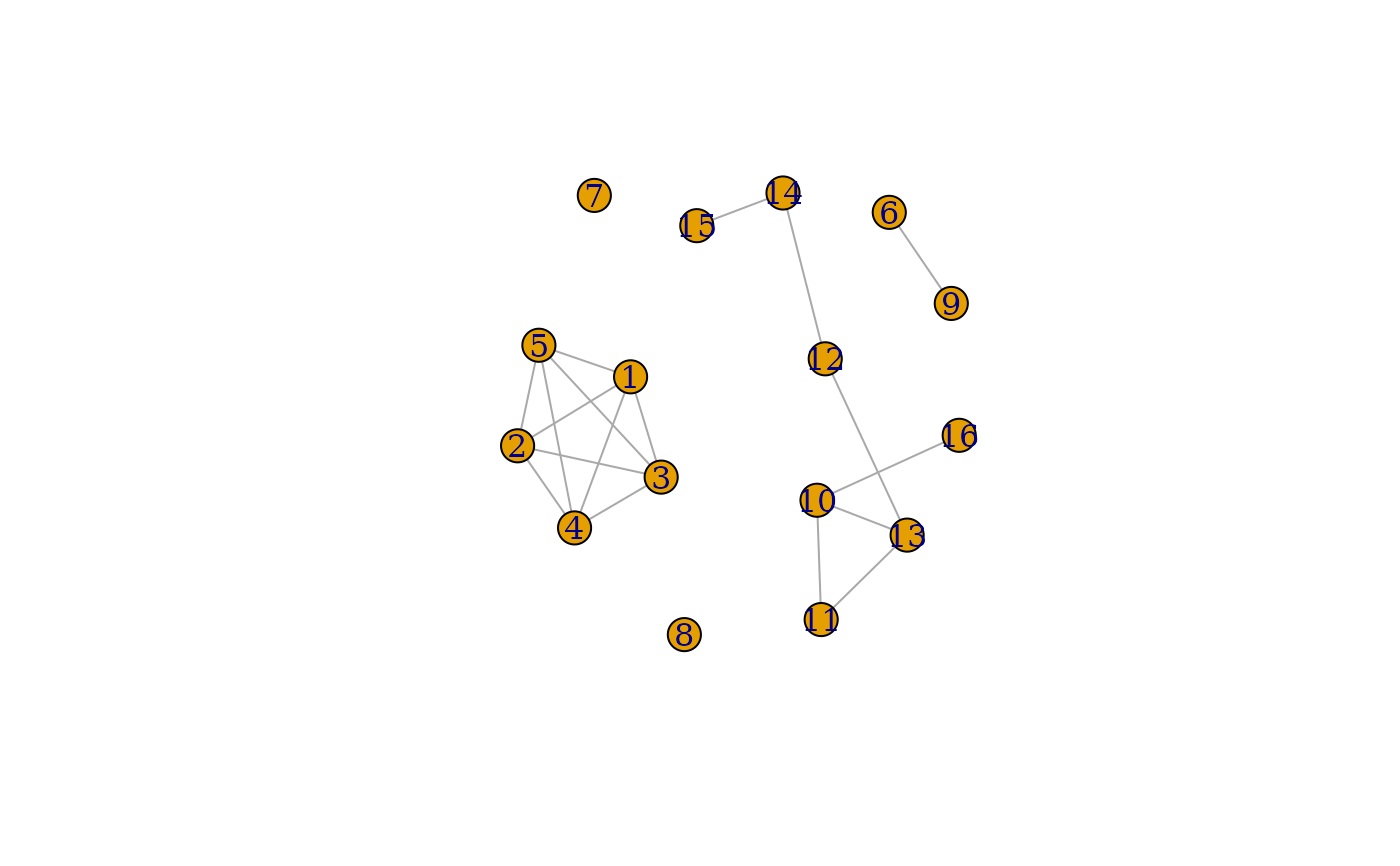
if (requireNamespace("igraph", quietly = TRUE)) {
G_strong <- igraph::simplify(
igraph::graph.adjacency(CS, weighted = TRUE, mode = "undirected")
)
plot(G_strong)
}
#> Warning: `graph.adjacency()` was deprecated in igraph 2.0.0.
#> ℹ Please use `graph_from_adjacency_matrix()` instead.