Causal inference is not just a statistics problem

Causal Inference is not a statistics problem

Causal Inference is not just a statistics problem

The problem

We have measured variables, what should we adjust for?

exposure outcome covariate
0.49 1.71 2.24
0.07 0.68 0.92
0.40 -1.60 -0.10
. . .
. . .
. . .
0.55 -1.73 -2.34

A bit more info

One unit increase in the exposure yields an average increase in the outcome of 1

cor(exposure, covariate)
[1] 0.7

The exposure and measured factor are positively correlated

To adjust or not adjust? That is the question.

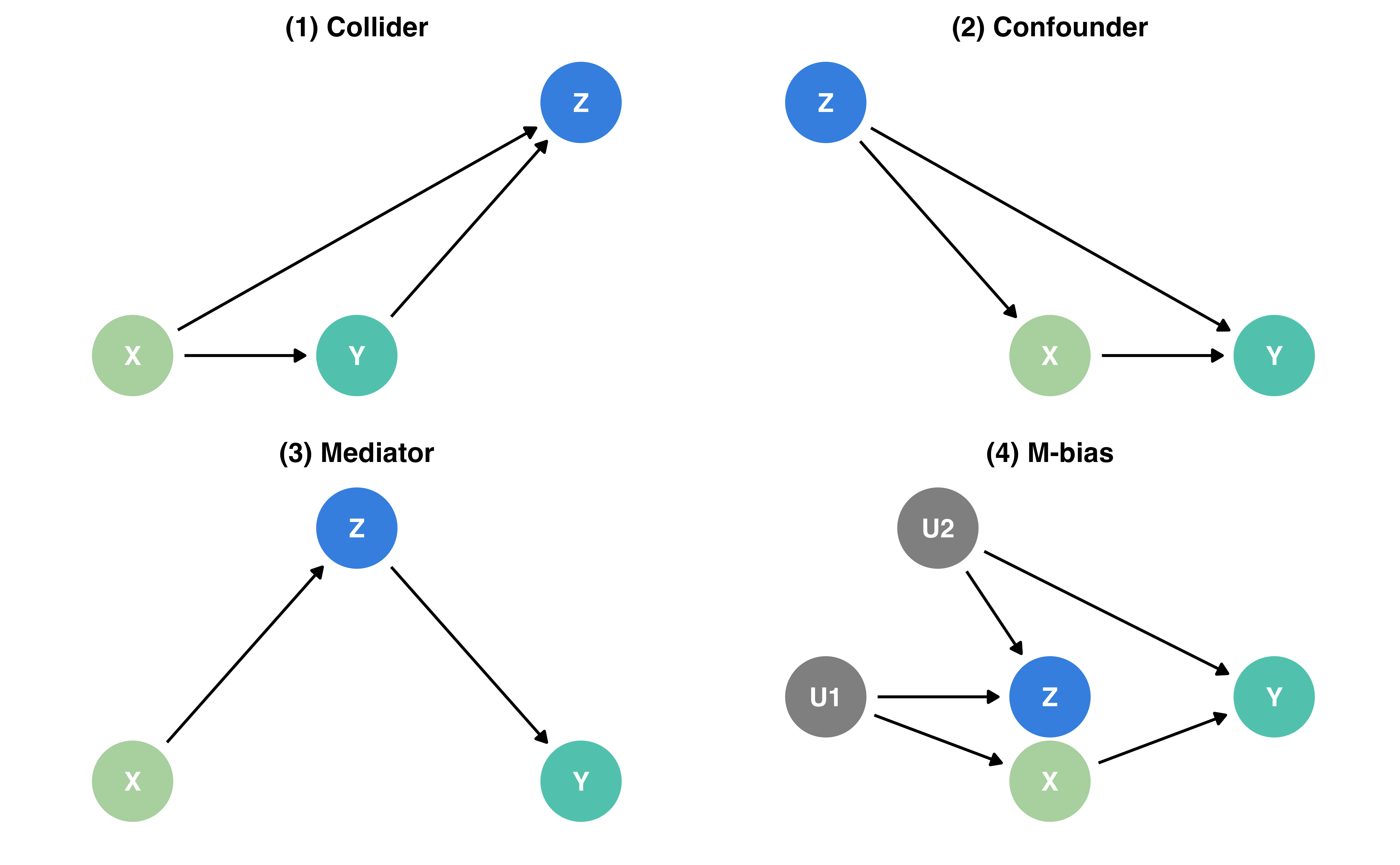
Causal Quartet

Your turn 1

Load the quartets package

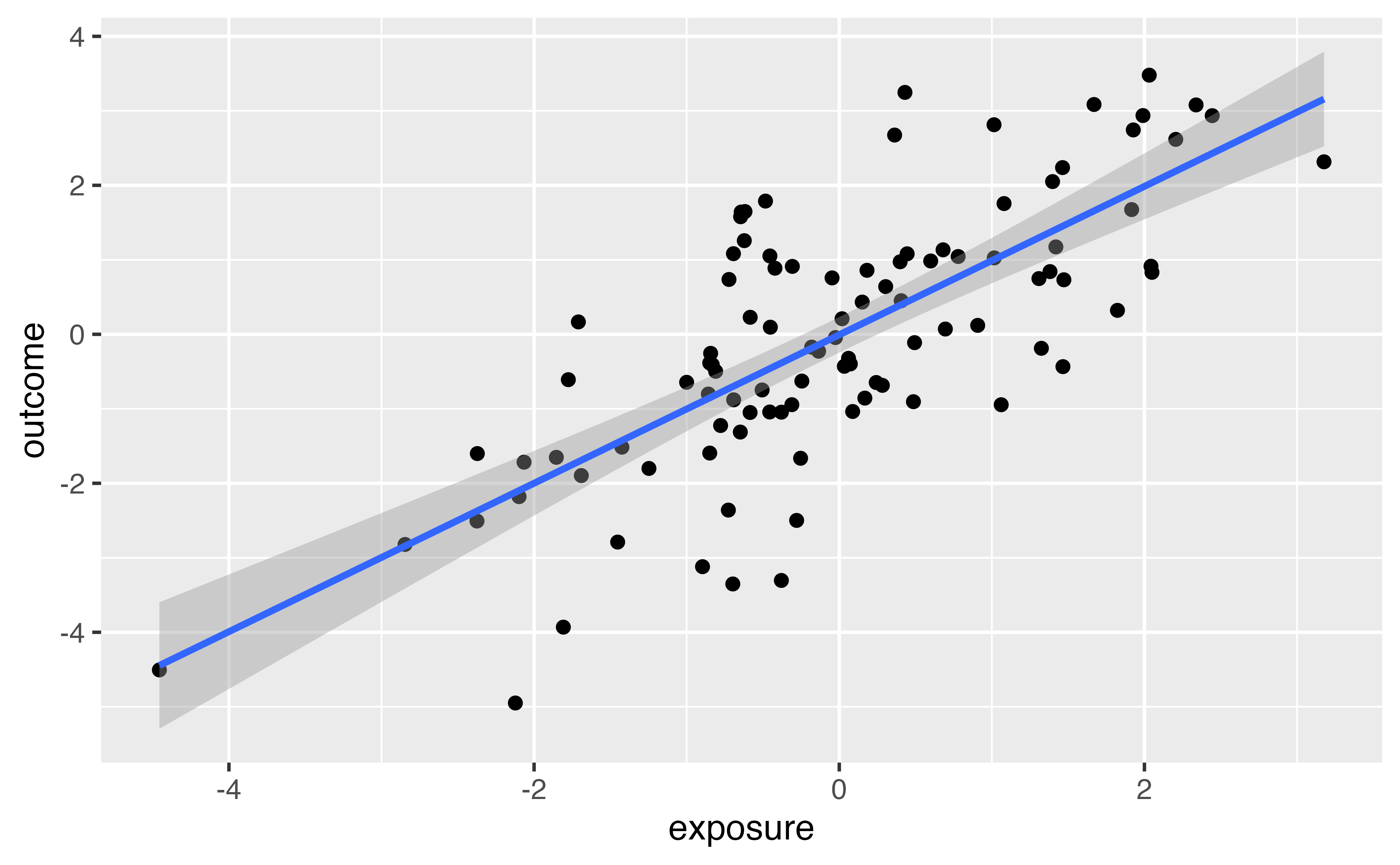
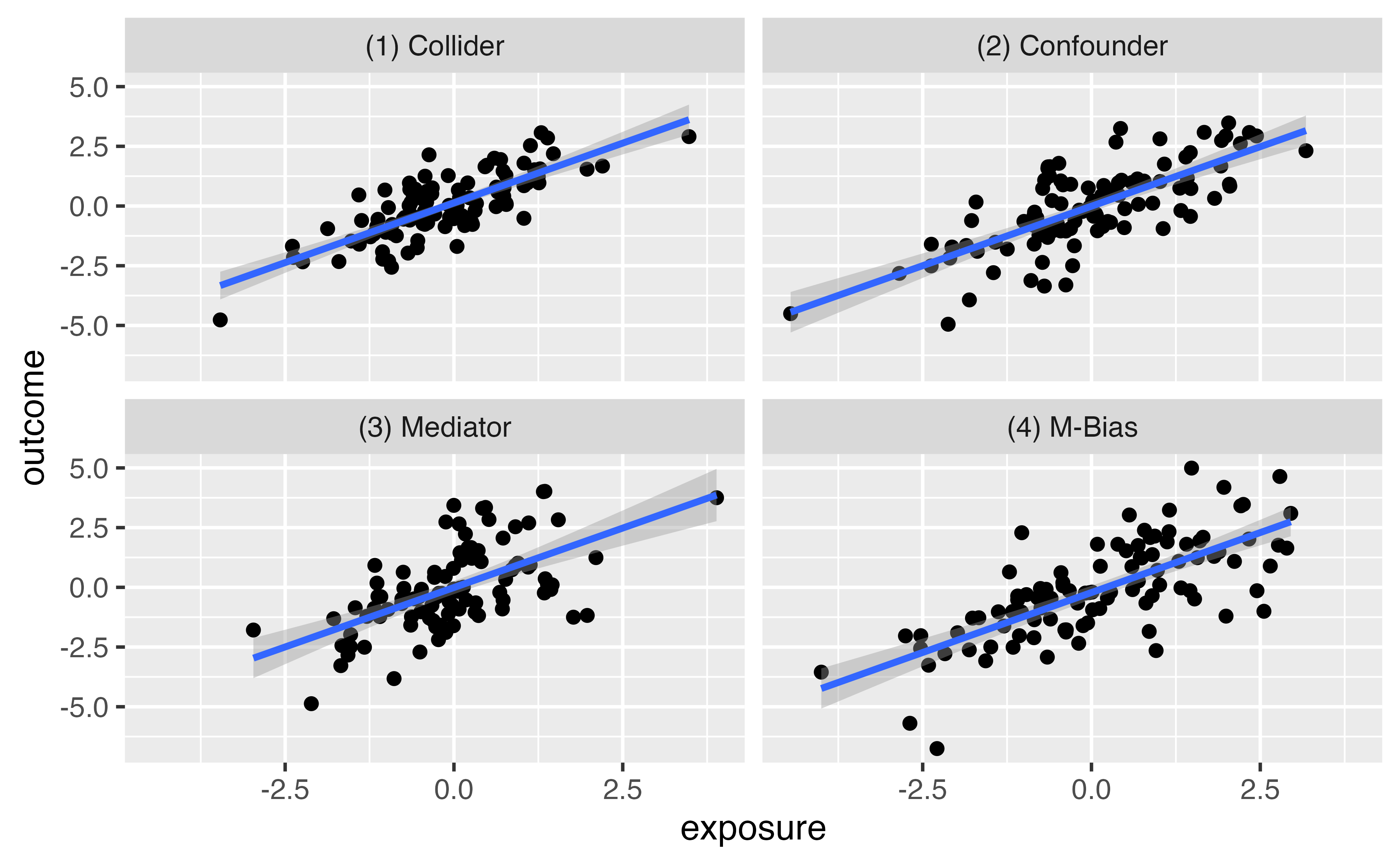
For each of the following 4 datasets, look at the correlation between exposure and covariate: causal_collider, causal_confounding, causal_mediator, causal_m_bias

For each of the above 4 datasets, create a scatterplot looking at the relationship between exposure and outcome

For each of the above 4 datasets, fit a linear model to examine the relationship between the exposure and the outcome

10:00

Relationship between exposure and outcome

Relationship between exposure and covariate

causal_quartet |>
  group_by(dataset) |>
  summarise(cor(exposure, covariate))
# A tibble: 4 × 2
  dataset        `cor(exposure, covariate)`
  <chr>                               <dbl>
1 (1) Collider                        0.700
2 (2) Confounder                      0.696
3 (3) Mediator                        0.696
4 (4) M-Bias                          0.696

Correct effects

Data generating mechanism Correct causal model Correct causal effect
(1) Collider Y ~ X 1.0
(2) Confounder Y ~ X ; Z 0.5
(3) Mediator Direct effect: Y ~ X ; Z Total Effect: Y ~ X Direct effect: 0.0 Total effect: 1.0
(4) M-Bias Y ~ X 1.0

D’Agostino McGowan L, Gerke T, Barrett M (2023). Causal inference is not a statistical problem. Preprint arXiv:2304.02683v1.

Observed effects

Data generating mechanism ATE not adjusting for Z ATE adjusting for Z Correlation of X and Z
(1) Collider 1.00 0.55 0.70
(2) Confounder 1.00 0.50 0.70
(3) Mediator 1.00 0.00 0.70
(4) M-Bias 1.00 0.88 0.70

D’Agostino McGowan L, Gerke T, Barrett M (2023). Causal inference is not a statistical problem. Preprint arXiv:2304.02683v1.

The solution

The partial solution

causal_collider_time
# A tibble: 100 × 6
   exposure_baseline outcome_baseline covariate_baseline
               <dbl>            <dbl>              <dbl>
 1          -1.43              0.287             -0.0963
 2           0.0593           -0.978             -1.11  
 3           0.370             0.348              0.647 
 4           0.00471           0.851              0.755 
 5           0.340             1.94               1.19  
 6          -3.61             -0.235             -0.588 
 7           1.44             -0.827             -1.13  
 8           1.02             -0.0410             0.689 
 9          -2.43             -2.10              -1.49  
10          -1.26             -2.41              -2.78  
# ℹ 90 more rows
# ℹ 3 more variables: exposure_followup <dbl>,
#   outcome_followup <dbl>, covariate_followup <dbl>

Time-varying data

Time-varying DAG

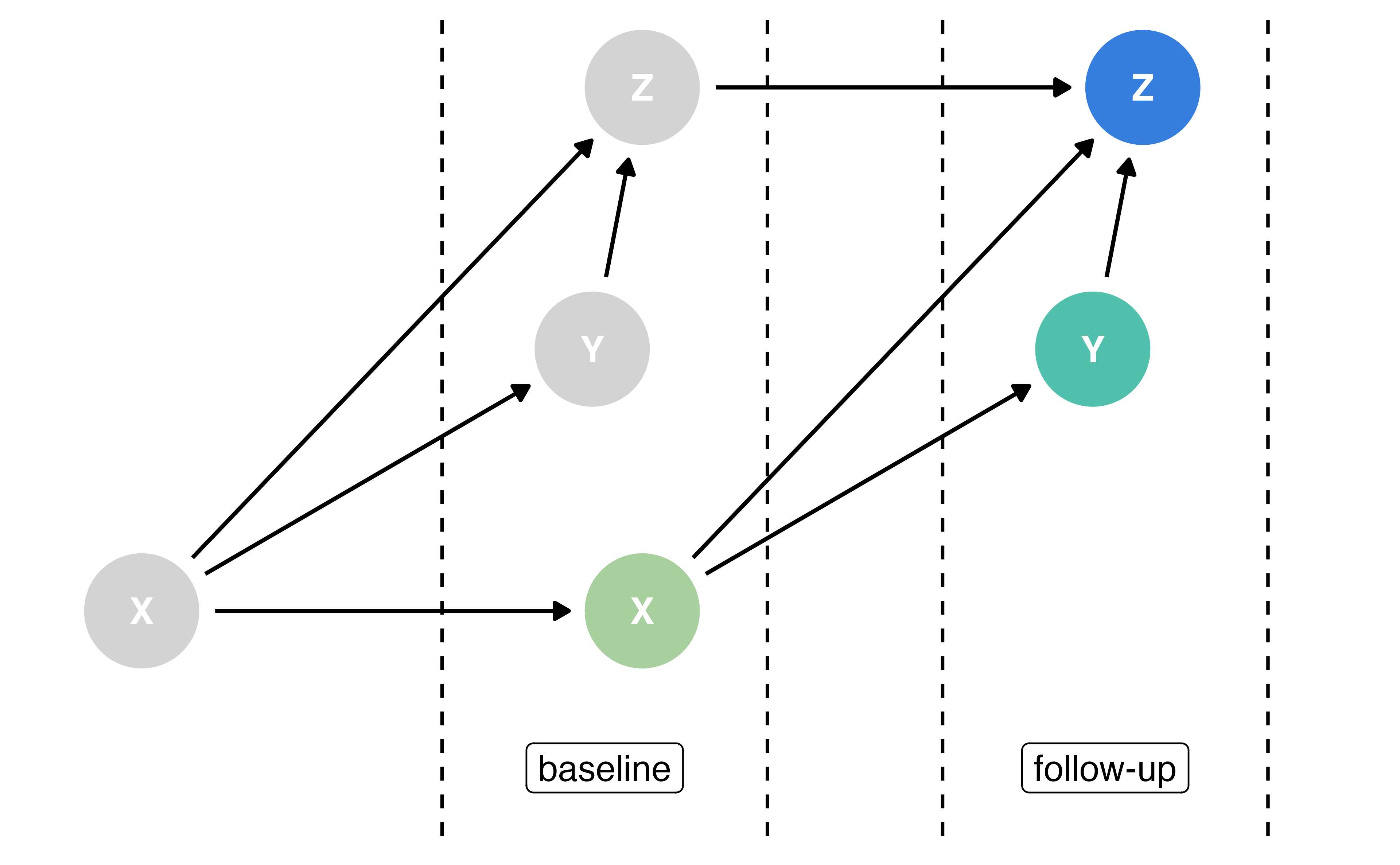
True causal effect: 1 Estimated causal effect: 0.55

Time-varying DAG

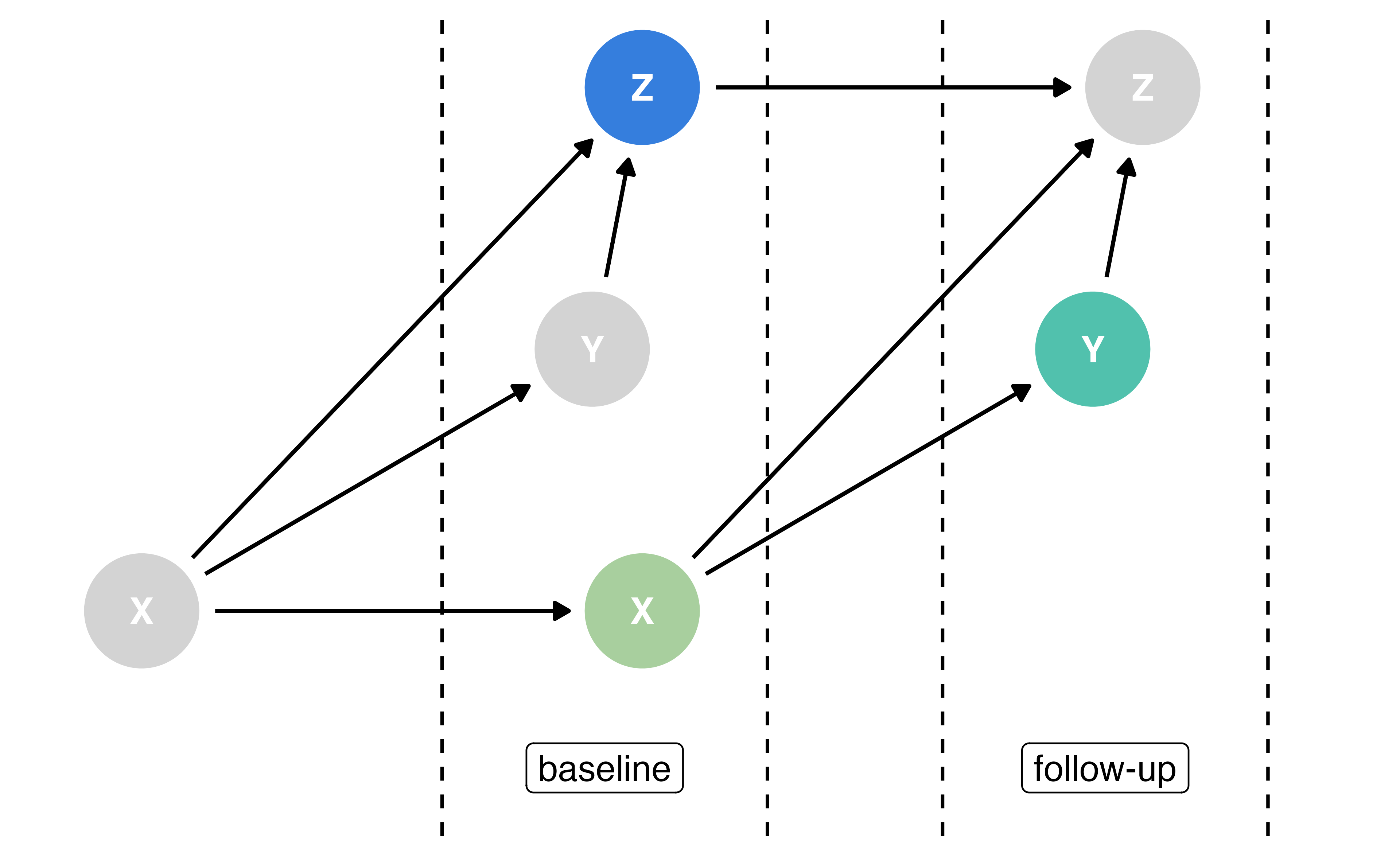
True causal effect: 1 Estimated causal effect: 1

outcome_followup ~ exposure_baseline + covariate_baseline

The partial solution

Data generating mechanism ATE not adjusting for pre-exposure Z ATE adjusting for pre-exposure Z Correct causal effect
(1) Collider 1.00 1.00 1.00
(2) Confounder 1.00 0.50 0.50
(3) Mediator 1.00 1.00 1.00
(4) M-Bias 1.00 0.88 1.00

D’Agostino McGowan L, Gerke T, Barrett M (2023). Causal inference is not a statistical problem. Preprint arXiv:2304.02683v1.

On M-Bias

  • The relationship between Z and the unmeasured confounders needs to be really large (Liu et al 2012)
  • “To obsess about the possibility of [M-bias] generates bad practical advice in all but the most unusual circumstances” (Rubin 2009)
  • There are (almost) no true zeros (Gelman 2011)
  • Asymptotic theory shows that induction of M-bias is quite sensitive to various deviations from the exact M-Structure (Ding and Miratrix 2014)

Your turn 2

For each of the following 4 datasets, fit a linear linear model examining the relationship between outcome_followup and exposure_baseline adjusting for covariate_baseline: causal_collider_time, causal_confounding_time, causal_mediator_time, causal_m_bias_time

10:00

Slides by Dr. Lucy D’Agostino McGowan